아래는 Python으로 빌드한 OpenCV 프로젝트(by 이세우) 제가 공부하고 정리한 것들입니다.
결정요인으로 표현할 수 없는 형태의 변형이 필요한 경우가 있습니다. 일반적인 예로는 투명한 물 유리에 반사된 장면이나 파도에 반사된 장면이 있습니다. 이 렌즈 왜곡 변환을 살펴보겠습니다.
12.1 리어트리뷰션
OpenCV는 규칙성 없이 모양을 마음대로 변환해주는 함수입니다. cv2.remap()이 기능은 기존 픽셀을 원하는 위치로 재배치합니다.
- dst = cv2.remap(src, mapx, mapy, interpolation(, dst, borderMode, borderValue))
- src: 입력 비디오
- mapx, mapy: x축과 y축을 따라 이동하기 위한 좌표(인덱스), src와 같은 크기, dtype=float32
- 나머지 인수는 cv2.warpAffine()과 동일합니다.
- dst: 결과 이미지
mapx와 mapy는 초기 값으로 0이나 1과 같은 의미 없는 값이 아닌 이미지의 원래 좌표 값을 갖는 것을 권장합니다. 모든 픽셀에서 이동하려는 몇 개의 픽셀에 대해서만 새 좌표를 지정하거나 원래 위치에서 일정량 이동하도록 요청하여 코딩하기가 더 쉽기 때문입니다.
np.indexes() 함수 사용 → 주어진 크기의 배열을 생성하고 인덱스를 값으로 초기화한 후 3D 배열로 반환합니다.
mapy, mapx = np.indices((rows, cols), dtype=np.float32)
cv2.remap() 함수는 예를 들어 이동할 좌표가 정수가 아니기 때문에 픽셀이 생략되면 자동으로 수정을 수행합니다.
cv2.remap() 함수를 사용하여 행렬식으로 표현할 수 있는 변환을 변환하는 것은 복잡하고 느립니다. 따라서 변환 행렬로 표현할 수 없는 비선형 변환에만 cv2.remap() 함수를 사용하는 것이 좋습니다. 이미징 분야에서 비선형 변환은 주로 렌즈 왜곡을 수정하거나 조작하는 데 사용됩니다.
12.2 오목 및 볼록 렌즈 왜곡
다시 매핑 기능을 사용하여 볼록 및 오목 렌즈 효과를 만들어 봅시다.
원 작업을 시작하기 전에 먼저 좌표계를 이해합시다.
원의 $p$ 지점을 가리키는 것은 두 가지로 표현할 수 있습니다.
- $(x, y)$ 좌표로 표현 직교 좌표계
- 원점 $O$에서 점 $p$까지의 거리와 각 $\theta$를 이용하여 $(r,\theta)$로 표현 극좌표계
두 좌표계는 다음 방정식에 의해 서로 변환될 수 있습니다.
- 직교좌표 → 극좌표: $\theta = arctan(x, y), r = \sqrt{x^2 + y^2}$
- 극좌표 → 데카르트 좌표: $x = rcos(\theta), y = rsin(\theta)$
OpenCV는 좌표를 변환하는 함수를 제공합니다.
- r, theta = cv2.cartToPolar(x, y) : 직교좌표의 변환 → 극좌표
- x, y = cv2.polarToCart(r, theta) : Polar → Cartesian 좌표 변환
- x, y : x, y 좌표의 배열
- r : 원점으로부터의 거리
- 세타 : 각도 값
데카르트 좌표를 극좌표로 변환하면 원 안의 픽셀만으로 작업하기 쉽고, 원점으로부터의 거리 $r$를 계산하여 원의 모양이나 면적을 쉽게 계산할 수 있습니다.
계산을 위해서는 좌표변환을 변경하는 것 뿐만 아니라 좌표의 기준점을 변경하는 것이 유리합니다. 이미지의 경우 데카르트 좌표를 사용하면 왼쪽 위 끝이 (0, 0) 좌표이지만 극좌표를 사용하면 이미지의 중심을 기준점으로 하는 것이 자연스럽고 음수 좌표 필요한 원점을 기준으로 왼쪽 및 아래쪽 지점에 사용됩니다. 따라서 좌표 값을 -1~1로 정규화하여 사용하는 것이 편리합니다.
exp에 대해 지수연산을 했을 때 지수값이 1보다 크면 중심의 밀도는 감소하고 주변으로 갈수록 밀도가 커지는 반면, 지수값이 1보다 작은 경우에는 그 반대가 된다. 밀도가 낮아질수록 픽셀 사이의 간격이 넓어지므로 확대 효과와 동일합니다.
12.3 방사형 왜곡
카메라 렌즈가 둥글고 이미지가 직사각형이기 때문에 렌즈 가장자리의 이미지에 왜곡이 있습니다. 이 왜곡을 **배럴 왜곡**이라고 합니다. 배럴 왜곡을 해결하기 위해 다음 방정식이 개발되었습니다.
$$ r_d = r_u (1 + k_1r^2_u + k_2r_u^4 + k_3r_u^6) $$
- $r_d$ : 워프 변환 후
- $r_u$ : 워프 변환 전
- $k_1, k_2, k_3$: 왜곡 계수
Barrel Distortion 계수의 값에 따라 Outward Barrel Distortion 또는 Inward Pincushion Distortion이 발생합니다.
OpenCV는 배럴 왜곡을 일으키는 렌즈 왜곡을 제거하는 것을 목표로 합니다. cv2.undistort() 기능을 제공합니다.
- dst = cv2.undistort(src, cameraMtrix, distCoeffs)
- src: 입력 소스 비디오
- cameraMatrix : 카메라 매트릭스
- $\begin{bmatrix} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}$
- distCoeffs : 왜곡 계수, 최소 4 또는 5, 8, 12, 14
- (k1, k2, p1, p2(, k3))
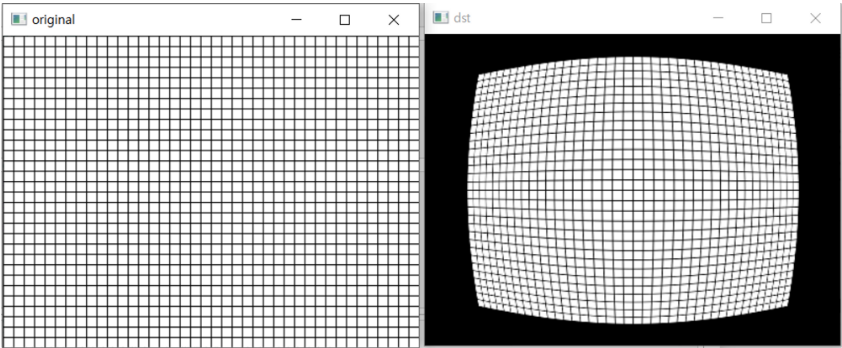
방사형 왜곡 효과
import cv2
import numpy as np
import matplotlib.pyplot as plt
# 격자 무늬 이미지 생성
img = np.full((300, 400, 3), 255, np.uint8)
img(::10, :, :) = 0
img(:, ::10, :) = 0
width = img.shape(1)
height = img.shape(0)
# 왜곡 계수 설정
k1, k2, p1, p2 = 0.001, 0, 0, 0 # 배럴 왜곡
# k1, k2, p1, p2 = -0.0005, 0, 0, 0 # 핀쿠션 왜곡
distCoeff = np.float64((k1, k2, p1, p2))
# 임의의 값으로 카메라 매트릭스 설정
fx, fy = 10, 10
cx, cy = width/2, height/2
camMtx = np.float32(((fx, 0, cx),
(0, fy, cy),
(0, 0, 1)))
# 왜곡 변형
dst = cv2.undistort(img, camMtx, distCoeff)
cv2.imshow('original', img)
cv2.imshow('dst', dst)
cv2.waitKey()
cv2.destroyAllWindows()